MKGeodesicPolyline

Written by Mattt April 28^th, 2014

We knew that the Earth was not flat long before 1492. Early navigators observed the way ships would dip out of view over the horizon many centuries before the Age of Discovery.

For many iOS developers, though, a flat MKMapView was a necessary conceit until recently.

What changed? The discovery of MKGeodesicPolyline, which is the subject of this week’s article.

MKGeodesicPolyline was introduced to the Map Kit framework in iOS 7. As its name implies, it creates a geodesic—essentially a straight line over a curved surface.

On the surface of a ~~sphere~~ ~~oblate spheroid~~ geoid, the shortest distance between two points appears as an arc on a flat projection. Over large distances, this takes a pronounced, circular shape.

An MKGeodesicPolyline is created with an array of 2 MKMapPoints or CLLocationCoordinate2Ds:

Creating an `MKGeodesicPolyline`

let LAX = CLLocation(latitude: 33.9424955, longitude: -118.4080684)
let JFK = CLLocation(latitude: 40.6397511, longitude: -73.7789256)

var coordinates = [LAX.coordinate, JFK.coordinate]
let geodesicPolyline = MKGeodesicPolyline(coordinates: &coordinates, count: 2)

mapView.addOverlay(geodesicPolyline)

CLLocation *LAX = [[CLLocation alloc] initWithLatitude:33.9424955
                                             longitude:-118.4080684];
CLLocation *JFK = [[CLLocation alloc] initWithLatitude:40.6397511
                                             longitude:-73.7789256];

CLLocationCoordinate2D coordinates[2] =
    {LAX.coordinate, JFK.coordinate};

MKGeodesicPolyline *geodesicPolyline =
    [MKGeodesicPolyline polylineWithCoordinates:coordinates
                                          count:2];

[mapView addOverlay:geodesicPolyline];

Although the overlay looks like a smooth curve, it is actually comprised of thousands of tiny line segments (true to its MKPolyline lineage):

print(geodesicPolyline.pointCount) // 3984

NSLog(@"%d", geodesicPolyline.pointCount) // 3984

Like any object conforming to the MKOverlay protocol, an MKGeodesicPolyline instance is displayed by adding it to an MKMapView with addOverlay() and implementing mapView(_:rendererForOverlay:):

Rendering `MKGeodesicPolyline` on an `MKMapView`

// MARK: MKMapViewDelegate

func mapView(mapView: MKMapView, rendererForOverlay overlay: MKOverlay) -> MKOverlayRenderer {
    guard let polyline = overlay as? MKPolyline else {
        return MKOverlayRenderer()
    }
    
    let renderer = MKPolylineRenderer(polyline: polyline)
    renderer.lineWidth = 3.0
    renderer.alpha = 0.5
    renderer.strokeColor = UIColor.blueColor()
    
    return renderer
}

#pragma mark - MKMap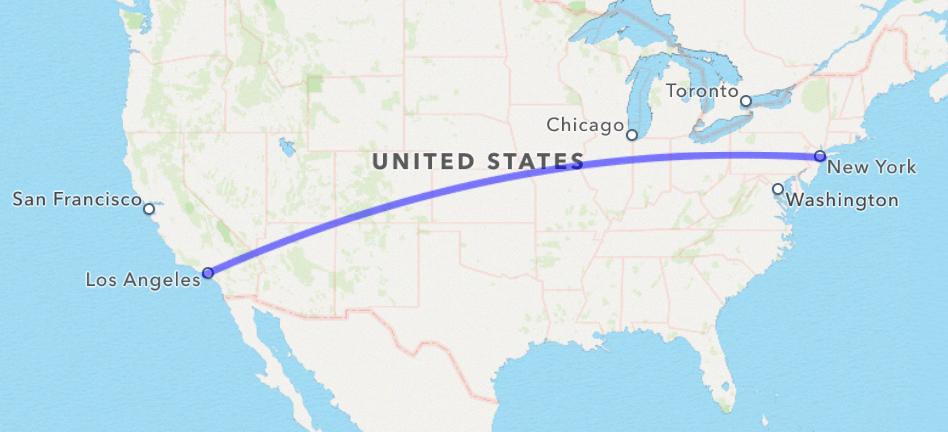ViewDelegate

- (MKOverlayRenderer *)mapView:(MKMapView *)mapView
            rendererForOverlay:(id <MKOverlay>)overlay
{
    if (![overlay isKindOfClass:[MKPolyline class]]) {
        return nil;
    }

    MKPolylineRenderer *renderer =
        [[MKPolylineRenderer alloc] initWithPolyline:(MKPolyline *)overlay];
    renderer.lineWidth = 3.0f;
    renderer.strokeColor = [UIColor blueColor];
    renderer.alpha = 0.5;

    return renderer;
}

MKGeodesicPolyline on an MKMapView

For comparison, here’s the same geodesic overlaid with a route created from MKDirections:

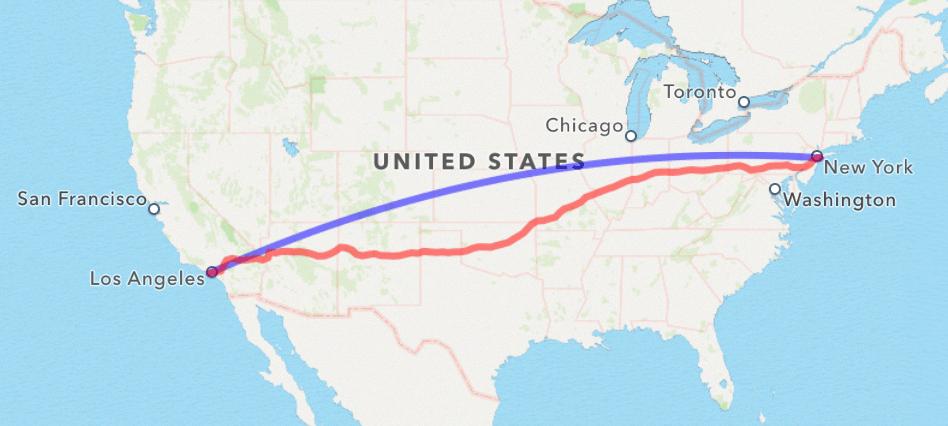
MKGeodesicPolyline on an MKMapView compared to MKDirections Polyline

As the crow flies, it’s 3,983 km.
As the wolf runs, it’s 4,559 km—nearly 15% longer.
…and that’s just distance; taking into account average travel speed, the total time is ~5 hours by air and 40+ hours by land.

Animating an `MKAnnotationView` on a `MKGeodesicPolyline`

Since geodesics make reasonable approximations for flight paths, a common use case would be to animate the trajectory of a flight over time.

To do this, we’ll make properties for our map view and geodesic polyline between LAX and JFK, and add new properties for the planeAnnotation and planeAnnotationPosition (the index of the current map point for the polyline):

// MARK: Flight Path Properties
var mapView: MKMapView!
var flightpathPolyline: MKGeodesicPolyline!
var planeAnnotation: MKPointAnnotation!
var planeAnnotationPosition = 0

@interface MapViewController () <MKMapViewDelegate>
@property MKMapView *mapView;
@property MKGeodesicPolyline *flightpathPolyline;
@property MKPointAnnotation *planeAnnotation;
@property NSUInteger planeAnnotationPosition;
@end

Next, right below the initialization of our map view and polyline, we create an MKPointAnnotation for our plane:

let annotation = MKPointAnnotation()
annotation.title = NSLocalizedString("Plane", comment: "Plane marker")
mapView.addAnnotation(annotation)

self.planeAnnotation = annotation
self.updatePlanePosition()

self.planeAnnotation = [[MKPointAnnotation alloc] init];
self.planeAnnotation.title = NSLocalizedString(@"Plane", nil);
[self.mapView addAnnotation:self.planeAnnotation];

[self updatePlanePosition];

That call to updatePlanePosition in the last line ticks the animation and updates the position of the plane:

func updatePlanePosition() {
    let step = 5
    guard planeAnnotationPosition + step < flightpathPolyline.pointCount
        else { return }

    let points = flightpathPolyline.points()
    self.planeAnnotationPosition += step
    let nextMapPoint = points[planeAnnotationPosition]
    
    self.planeAnnotation.coordinate = MKCoordinateForMapPoint(nextMapPoint)
    
    performSelector("updatePlanePosition", withObject: nil, afterDelay: 0.03)
}

- (void)updatePlanePosition {
    static NSUInteger const step = 5;

    if (self.planeAnnotationPosition + step >= self.flightpathPolyline.pointCount) {
        return;
    }

    self.planeAnnotationPosition += step;
    MKMapPoint nextMapPoint = self.flightpathPolyline.points[self.planeAnnotationPosition];

    self.planeAnnotation.coordinate = MKCoordinateForMapPoint(nextMapPoint);

    [self performSelector:@selector(updatePlanePosition) withObject:nil afterDelay:0.03];
}

We’ll perform this method roughly 30 times a second, until the plane has arrived at its final destination.

Finally, we implement mapView(_:viewForAnnotation:) to have the annotation render on the map view:

func mapView(mapView: M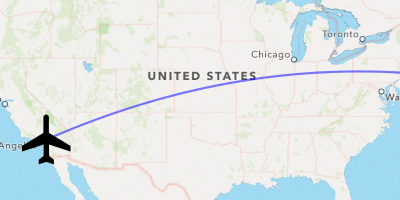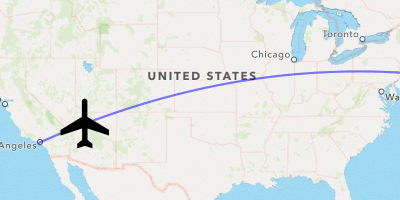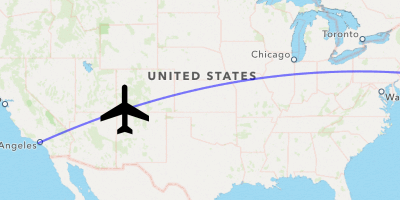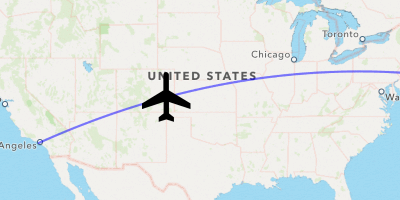KMapView, viewForAnnotation annotation: MKAnnotation) -> MKAnnotationView? {
    let planeIdentifier = "Plane"
    
    let annotationView = mapView.dequeueReusableAnnotationViewWithIdentifier(planeIdentifier)
            ?? MKAnnotationView(annotation: annotation, reuseIdentifier: planeIdentifier)
    
    annotationView.image = UIImage(named: "airplane")

    return annotationView
}

- (MKAnnotationView *)mapView:(MKMapView *)mapView
            viewForAnnotation:(id <MKAnnotation>)annotation
{
    static NSString * PinIdentifier = @"Pin";

    MKAnnotationView *annotationView = [mapView dequeueReusableAnnotationViewWithIdentifier:PinIdentifier];
    if (!annotationView) {
        annotationView = [[MKAnnotationView alloc] initWithAnnotation:annotation reuseIdentifier:PinIdentifier];
    }

    annotationView.image = [UIImage imageNamed:@"plane"];

    return annotationView;
}

MKAnnotationView without Rotation

Hmm… close but no SkyMall Personalized Cigar Case Flask.

Let’s update the rotation of the plane as it moves across its flightpath.

Rotating an `MKAnnotationView` along a Path

To calculate the plane’s direction, we’ll take the slope from the previous and next points:

let previousMapPoint = points[planeAnnotationPosition]
planeAnnotationPosition += step
let nextMapPoint = points[planeAnnotationPosition]

self.planeDirection = directionBetweenPoints(previousMapPoint, nextMapPoint)
self.planeAnnotation.coordinate = MKCoordinateForMapPoint(nextMapPoint)

MKMapPoint previousMapPoint = self.flightpathPolyline.points[self.planeAnnotationPosition];
self.planeAnnotationPosition += step;
MKMapPoint nextMapPoint = self.flightpathPolyline.points[self.planeAnnotationPosition];

self.planeDirection = XXDirectionBetweenPoints(previousMapPoint, nextMapPoint);
self.planeAnnotation.coordinate = MKCoordinateForMapPoint(nextMapPoint);

directionBetweenPoints is a function that returns a CLLocationDirection (0 – 360 degrees, where North = 0) given two MKMapPoints.

We calculate from MKMapPoints rather than converted coordinates, because we’re interested in the slope of the line on the flat projection.

private func directionBetweenPoints(sourcePoint: MKMapPoint, _ destinationPoint: MKMapPoint) -> CLLocationDirection {
    let x = destinationPoint.x - sourcePoint.x
    let y = destinationPoint.y - sourcePoint.y
    
    return radiansToDegrees(atan2(y, x)) % 360 + 90
}

static CLLocationDirection XXDirectionBetweenPoints(MKMapPoint sourcePoint, MKMapPoint destinationPoint) {
    double x = destinationPoint.x - sourcePoint.x;
    double y = destinationPoint.y - sourcePoint.y;

    return fmod(XXRadiansToDegrees(atan2(y, x)), 360.0f) + 90.0f;
}

That convenience function radiansToDegrees (and its partner, degreesToRadians) are simply:

private func radiansToDegrees(radians: Double) -> Double {
    return radians * 180 / M_PI
}

private func degreesToRadians(degrees: Double) -> Double {
    return degrees * M_PI / 180
}

static inline double XXRadiansToDegrees(double radians) {
    return radians * 180.0f / M_PI;
}

static inline double XXDegreesToRadians(double degrees) {
    return degrees * M_PI / 180.0f;
}

That direction is stored in a new property, var planeDirection: CLLocationDirection, calculated from self.planeDirection = directionBetweenPoints(currentMapPoint, nextMapPoint) in updatePlanePosition (ideally renamed to updatePlanePositionAndDirection with this addition). To make the annotation rotate, we apply a transform on annotationView:

annotationView.transform = CGAffineTransformRotate(mapView.transform, 
        degreesToRadians(planeDirection))

self.annotation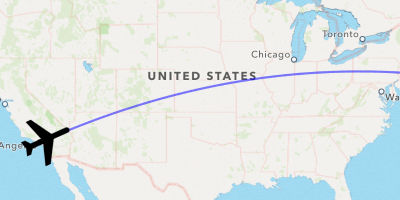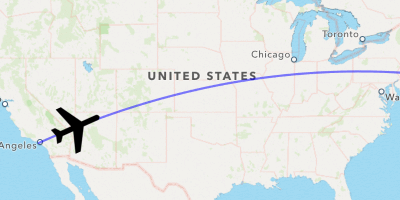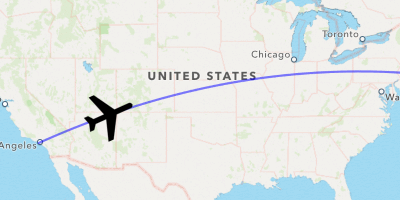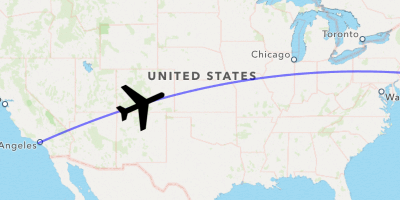View.transform =
    CGAffineTransformRotate(self.mapView.transform,
                            XXDegreesToRadians(self.planeDirection));

MKAnnotationView with Rotation

Ah much better! At last, we have mastered the skies with a fancy visualization, worthy of any travel-related app.

Perhaps more than any other system framework, MapKit has managed to get incrementally better, little by little with every iOS release [1] [2]. For anyone with a touch-and-go relationship to the framework, returning after a few releases is a delightful experience of discovery and rediscovery.

I look forward to seeing what lies on the horizon with iOS 8 and beyond.

Creating an MKGeodesicPolyline

Rendering MKGeodesicPolyline on an MKMapView

Animating an MKAnnotationView on a MKGeodesicPolyline

Rotating an MKAnnotationView along a Path

Creating an `MKGeodesicPolyline`

Rendering `MKGeodesicPolyline` on an `MKMapView`

Animating an `MKAnnotationView` on a `MKGeodesicPolyline`

Rotating an `MKAnnotationView` along a Path